Erklärbare Künstliche Intelligenz (engl. Explainable Artificial Intelligence, kurz XAI) ist ein wichtiges Teilgebiet der Künstlichen Intelligenz, das sich darauf konzentriert, Entscheidungsprozesse von maschinellen Lernverfahren für den Menschen nachvollziehbar zu machen. Dies ist besonders wichtig für Black-Box-Modelle, wie Ensemble- oder Deep-Learning-Algorithmen, die aufgrund ihrer Komplexität selbst von Experten nicht verstanden werden können (siehe auch meinen Artikel über Erklärbare Künstliche Intelligenz). Ein besseres Verständnis solcher Black-Box-Modelle führt unter anderem zu mehr Vertrauen bei den Anwendern und gibt Hinweise, wie ein Modell verbessert werden kann.
Eine beliebte Methode der Erklärbaren Künstlichen Intelligenz ist SHAP (SHapley Additive ExPlanations). SHAP kann auf beliebige Modelle des maschinellen Lernens angewendet werden und erklärt, wie einzelne Merkmale (engl. Features) die Vorhersagen eines Modells beeinflussen. Diese Beitragsreihe gibt Dir eine leicht verständliche Einführung in die Erklärungsmethode SHAP und das spieltheoretische Konzept der Shapley-Werte, das dabei eine zentrale Rolle spielt. Außerdem lernst Du anhand eines praktischen Programmierbeispiels, wie Du die Vorhersagen von Black-Box-Modellen mit Hilfe der Python-Bibliothek SHAP erklären kannst. Die Beitragsreihe besteht aus den folgenden 3 Artikeln:
- Wie kann man Black-Box-Modelle mit Shapley-Werten erklären?
- Der ultimative Leitfaden, um SHAP mit Leichtigkeit zu meistern
- Ein umfassendes Python-Tutorial zum schnellen Einstieg in SHAP
Dies ist der dritte Artikel dieser Beitragsreihe. In diesem Artikel erfährst Du, wie die Python-Bibliothek SHAP verwendet werden kann, um maschinelle Lernverfahren zu erklären. Anhand eines einfachen Programmierbeispiels lernst Du, wie mit Hilfe der Python-Bibliothek SHAP Feature-Attributionen berechnet und interpretiert werden können. Außerdem erfährst Du, welche Visualisierungen die Python-Bibliothek SHAP bietet und wie diese für lokale und globale Erklärungen verwendet werden können. Am Ende dieses Artikels wirst Du ein solides Verständnis der Funktionalität der Python-Bibliothek SHAP haben und wissen, wie sie Dir helfen kann, Black-Box-Modelle besser zu verstehen. Den Python-Code zu diesem Artikel findest Du auch auf GitHub oder in diesem Google Colab Notebook.
Überblick
Dieser Blog-Artikel ist in die folgenden Abschnitte unterteilt:
- Was ist die Python-Bibliothek SHAP?
- Training eines XGBoost-Modells für den California Housing Datensatz
- Wie berechnet man Feature-Attributionen mit der Python-Bibliothek SHAP?
- Wie erzeugt man lokale Erklärungen mit der Python-Bibliothek SHAP?
- Wie erstellt man globale Erklärungen mit der Python-Bibliothek SHAP?
Was ist die Python-Bibliothek SHAP?
SHAP ist ein Sammelbegriff für verschiedene Methoden zur Schätzung von Shapley-Werten. Shapley-Werte helfen, besser zu verstehen, wie ein maschinelles Lernmodell zu seinen Entscheidungen kommt. Shapley-Werte geben nicht nur Auskunft über die Wichtigkeit von Merkmalen, sondern insbesondere auch darüber, wie einzelne Merkmale die Vorhersagen eines Modells beeinflussen. Die Beiträge der Merkmale zu einer Modellvorhersage werden auch als Feature-Attributionen bezeichnet.
Shapley-Werte können sowohl für lokale als auch für globale Erklärungen verwendet werden. Während lokale Erklärungen helfen, einzelne Vorhersagen eines Modells zu verstehen, tragen globale Erklärungen zum Verständnis des Gesamtverhaltens eines Modells bei. Darüber hinaus ist SHAP eine modellagnostische Erklärungsmethode, d.h. sie kann auf beliebige Algorithmen des maschinellen Lernens angewendet werden.
Wir verwenden im Folgenden die Python-Bibliothek SHAP, um Shapley-Werte für ein Regressionsmodell zur Vorhersage von Hauspreisen zu berechnen. Die Python-Bibliothek SHAP kann jedoch analog auch für Klassifikationsmodelle verwendet werden. Neben der Implementierung verschiedener SHAP-Methoden stellt die Bibliothek auch zahlreiche Visualisierungen zur Verfügung. Mit Hilfe dieser Visualisierungen können sowohl lokale als auch globale Erklärungen generiert werden. Die wichtigsten Funktionalitäten der Python-Bibliothek SHAP sind in Abbildung 1 dargestellt.
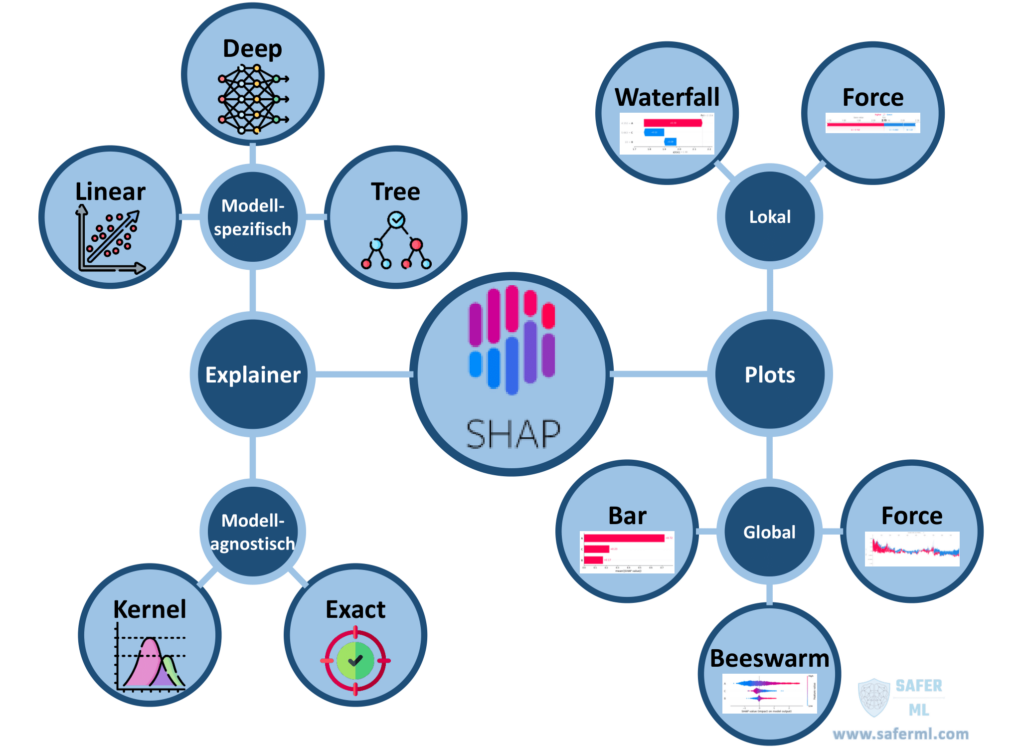
Training eines XGBoost-Modells für den California Housing Datensatz
Das maschinelle Lernverfahren, dessen Entscheidungsprozess wir in diesem Tutorial erklären wollen, ist ein XGBoost (Extreme Gradient Boosting) Modell. XGBoost ist ein schnelles und leistungsfähiges Ensemble-Verfahren, das Entscheidungsbäume als schwache Lerner verwendet und deren Vorhersagen durch Gradient Boosting zu einem präzisen Vorhersagemodell kombiniert. Der XGBoost-Algorithmus ist ein sehr beliebtes maschinelles Lernverfahren und eignet sich sowohl für Regressions- als auch für Klassifikationsaufgaben.
Seine Popularität rührt daher, dass XGBoost bei vielen Benchmark-Datensätzen eine bessere Leistung zeigt als andere maschinelle Lernverfahren. Beispielsweise hat XGBoost mehr Kaggle-Wettbewerbe gewonnen als jedes andere maschinelle Lernverfahren. XGBoost ist somit der State of the Art Algorithmus für Probleme mit strukturierten Daten. Damit ist der XGBoost-Algorithmus auch perfekt für den Datensatz geeignet, mit dem wir in diesem Tutorial arbeiten werden.
Installation der benötigten Python-Bibliotheken
Um SHAP in Python verwenden zu können, musst Du zunächst die Python-Bibliothek SHAP installieren. Dies kannst Du entweder mit pip oder mit conda tun:
pip install shap
or
conda install -c conda-forge shapIm nächsten Schritt werden alle benötigten Bibliotheken importiert:
# We use the SHAP library to estimate and visualize Shapley values
import shap
# We use the XGBoost implementation from the xgboost library
import xgboost
# We use this function from the Scikit-learn library to split our dataset into a training dataset and a test dataset
from sklearn.model_selection import train_test_split
# We use this function from the Scikit-learn library to compute the mean squared error of the model's predictions
from sklearn.metrics import mean_squared_errorWir benötigen die Bibliothek SHAP, um die Shapley-Werte zu berechnen. Außerdem benötigen wir die Bibliothek xgboost für unser XGBoost-Modell. Um unseren Datensatz in Trainings- und Testdaten aufzuteilen, verwenden wir die entsprechende Funktion aus der Bibliothek sklearn. Schließlich benötigen wir noch eine weitere Funktion aus sklearn, um den Mean Squared Error (MSE) für unser Modell berechnen zu können.
Der California Housing Datensatz
Als Datensatz verwenden wir den California Housing Datensatz . Dieser Datensatz enthält Informationen über 20.640 Blockgruppen in ganz Kalifornien aus dem Jahr 1990. Unser Ziel ist es, ein Regressionsmodell zu trainieren, um den natürlichen Logarithmus des medianen Hauspreises für verschiedene Blockgruppen zu schätzen. Die acht Merkmale, die uns zu diesem Zweck zur Verfügung stehen, sind in Tabelle 1 aufgeführt.
| Name des Merkmals | Beschreibung |
|---|---|
| MedInc | Medianeinkommen in der Blockgruppe |
| HouseAge | Medianalter der Häuser in der Blockgruppe |
| AveRooms | Durchschnittliche Anzahl der Räume pro Haushalt |
| AveBedrms | Durchschnittliche Anzahl der Schlafzimmer pro Haushalt |
| Population | Einwohnerzahl in der Blockgruppe |
| AveOccup | Durchschnittliche Zahl der Haushaltsmitglieder |
| Latitude | Breitengrad der Blockgruppe |
| Longitude | Längengrad der Blockgruppe |
Der California Housing Datensatz ist direkt in der Python-Bibliothek SHAP enthalten und kann daher einfach importiert werden:
# Load the California housing dataset
# X is the features and y is the targets
X, y = shap.datasets.california()X ist die Merkmalsmatrix und der Vektor y ist die Zielvariable, welche die durchschnittlichen Hauspreise der verschiedenen Blockgruppen enthält.
Training des XGBoost-Modells
Um unser XGBoost-Modell auf diesem Datensatz zu trainieren, unterteilen wir den Datensatz zunächst in einen Trainings- und einen Testdatensatz. Während der Trainingsdatensatz dazu dient, die Parameter des XGBoost-Modells optimal zu kalibrieren, wird der Testdatensatz lediglich zur Evaluierung des Modells verwendet. Um den Datensatz in einen Trainings- und einen Testdatensatz aufzuteilen, verwenden wir die Funktion „train_test_split“ aus der Bibliothek sklearn:
# Split the dataset into a training dataset and a test dataset, using 80% of the instances for the training dataset and 20% of the instances for the test dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)Durch die Wahl des Parameters „test_size=0.2“ wurde der Datensatz so aufgeteilt, dass der Testdatensatz 20% der Instanzen des Originaldatensatzes und der Trainingsdatensatz die restlichen 80% der Instanzen enthält. Durch die Wahl eines festen Wertes für den Parameter „random_state“ bleibt die Aufteilung des Datensatzes reproduzierbar.
Im nächsten Schritt können wir unseren Trainingsdatensatz verwenden, um das XGBoost-Modell zu trainieren. Dazu muss zunächst ein XGBoost-Modell initialisiert werden. Da es sich um ein Regressionsproblem handelt, verwenden wir den XGBRegressor:
# Initialize an XGBoost model for regression tasks
model = xgboost.XGBRegressor()Nach der Initialisierung können wir das Modell einfach mit der Fit-Funktion auf unseren Trainingsdatensatz trainieren:
# Train the XGBoost model on the training dataset
model.fit(X_train, y_train)Um sicherzustellen, dass das Modell nicht überangepasst ist, sollten wir die Leistung des Modells auf den Testdaten evaluieren. Dazu prognostizieren wir zunächst die durchschnittlichen Hauspreise für alle Blockgruppen des Testdatensatzes:
# Make predictions on the test dataset using the XGBoost model
predictions = model.predict(X_test)Um die Abweichung der Modellvorhersagen von der tatsächlichen Zielvariable zu beurteilen, berechnen wir den Mean Squared Error (MSE):
# Calculate the prediction error for the test dataset using the mean squared error
mse = mean_squared_error(y_test, predictions)
print(f"MSE: {mse}")Sehr gut, unser Modell erreicht auf den Testdaten einen MSE von 0,21!
Wie berechnet man Feature-Attributionen mit der Python-Bibliothek SHAP?
Nun können wir die Python-Bibliothek SHAP verwenden, um Erklärungen für das trainierte XGBoost-Modell zu generieren, die uns helfen, das Verhalten des Modells besser zu verstehen. In der SHAP-Bibliothek sind verschiedene SHAP-Methoden implementiert. Die drei wichtigsten sind die Explainer „Tree“, „Deep“ und „Kernel“.
Die Explainer-Klasse „Tree“ ist eine Implementierung von Tree SHAP und ermöglicht die schnelle und genaue Berechnung von Shapley-Werten für baumbasierte maschinelle Lernverfahren wie Entscheidungsbäume, Random Forests und XGBoost. Die Explainer-Klasse „Deep“ hingegen entspricht dem Deep SHAP Algorithmus und ist somit auf die schnelle Berechnung von Shapley-Werten für Deep-Learning-Modelle spezialisiert.
Der Kernel-SHAP-Algorithmus ist in der Explainer-Klasse „Kernel“ implementiert und ermöglicht die Approximation von Shapley-Werten für beliebige maschinelle Lernverfahren. Damit können z.B. auch Shapley-Werte für Algorithmen wie K-Nearest-Neighbor (KNN) berechnet werden. Allerdings ist die Kernel-SHAP-Methode deutlich langsamer als die beiden anderen modellspezifischen Explainer-Klassen.
Zusätzlich gibt es den Explainer „Exact“, mit dem die Shapley-Werte für ein Modell exakt berechnet werden können. Dies ist jedoch nur für kleine Datensätze mit weniger als 15 Merkmalen sinnvoll. Ansonsten ist die Berechnung der exakten Shapley-Werte mit sehr langen Rechenzeiten verbunden.
Auswahl der richtigen Explainer-Klasse
Im Allgemeinen brauchst Du Dir keine großen Gedanken über die Wahl des SHAP-Algorithmus zu machen. Du kannst einfach die allgemeine Explainer-Klasse der Python-Bibliothek SHAP verwenden, um Shapley-Werte für dein Modell zu berechnen. Diese Klasse wählt dann standardmäßig die am besten geeignete SHAP-Methode aus, um die Shapley-Werte zu approximieren, abhängig von Deinem Modell und der Größe Deiner Daten. Das Tolle an der SHAP-Bibliothek ist, dass sie mit verschiedenen Machine Learning Frameworks kompatibel ist, darunter sklearn, Tensorflow und PyTorch.
Um die Shapley-Werte für unser XGBoost-Modell zu berechnen, müssen wir zunächst den SHAP-Explainer initialisieren. Als Modell geben wir unser XGBoost-Modell an (Parameter „model“). Für den Parameter „masker“ geben wir den Datensatz an, aus dem der Basiswert für die Shapley-Werte geschätzt werden soll. Wie Du sicher noch aus meinem Artikel über Shapley-Werte weißt, sind Shapley-Werte immer relativ zu einem Basiswert. Der Basiswert ist der Mittelwert aller Vorhersagen des Modells für die Instanzen des Datensatzes, den wir bei der Initialisierung des Explainer-Objekts als Parameter „masker“ angeben. Wir verwenden dazu den Trainingsdatensatz.
# Initialize an explainer that estimates Shapley values using SHAP
# Here we use the training dataset X_train to compute the base value
explainer = shap.Explainer(model=model, masker=X_train) Der Explainer wählt automatisch eine geeignete SHAP-Methode für unser Modell und unsere Daten aus. Die gewählte Methode kannst Du Dir über das Attribut „__class__“ des Explainer anzeigen lassen:
explainer.__class__Wie Du siehst, wurde automatisch der Algorithmus Tree SHAP ausgewählt. Dies ist sinnvoll, da es sich bei XGBoost um ein Ensemble von Entscheidungsbäumen handelt. Für solche Modelle können mit Tree SHAP die Shapley-Werte sehr schnell und mit hoher Genauigkeit approximiert werden.
Berechnung von Shapley-Werten mit dem SHAP-Explainer
Der Explainer kann entweder zur Berechnung von Shapley-Werten für einzelne Instanzen oder für ganze Datensätze verwendet werden. In unserem Fall berechnen wir Shapley-Werte für alle Instanzen des Testdatensatzes. Dazu müssen wir nur den Explainer auf den Testdatensatz anwenden:
# Estimate the Shapley values for the test dataset
shap_values = explainer(X_test)Nach der Berechnung der Shapley-Werte gibt der Explainer ein Objekt zurück, das wir „shap_values“ genannt haben. Dieses Objekt besteht aus folgenden Attributen:
- shap_values.values: Dies ist eine Matrix, welche die Shapley-Werte für jede Instanz der Eingabedaten enthält, d.h. in unserem Fall die Shapley-Werte für alle Instanzen des Testdatensatzes. Die Matrix hat dieselben Dimensionen wie der Testdatensatz. Die Anzahl der Spalten entspricht der Anzahl der Merkmale (in unserem Fall 8) und die Anzahl der Zeilen entspricht der Anzahl der Instanzen in unserem Testdatensatz. Jede Zeile der Matrix enthält die Shapley-Werte für genau eine Instanz des Testdatensatzes und deren Merkmalsausprägungen.
- shap_values.base_values: Dies ist ein Vektor, der den Basiswert enthält. Die Dimension des Vektors entspricht der Anzahl der Instanzen in den Eingabedaten. Da der Basiswert für alle Instanzen gleich ist, entsprechen alle Einträge dieses Vektors dem gleichen Wert. Dieser Wert ist der Mittelwert aller Vorhersagen des Modells für den Datensatz, der bei der Erstellung des Explainer-Objekts im Parameter „masker“ angegeben wurde (in unserem Fall der Trainingsdatensatz).
- shap_values.data: Dies ist einfach eine Kopie der Eingabedaten, d.h. in unserem Fall des Testdatensatzes.
Wir wollen nun die berechneten Shapley-Werte verwenden, um das Modellverhalten besser zu verstehen. Dabei können wir die Shapley-Werte sowohl für lokale als auch für globale Erklärungen verwenden. Lokale Erklärungen helfen uns, den Einfluss verschiedener Merkmale auf einzelne Modellvorhersagen besser zu verstehen. Globale Erklärungen helfen uns, das Verhalten des Modells als Ganzes zu verstehen. Im Folgenden werden verschiedene Visualisierungen für lokale und globale Erklärungen betrachtet, die uns die Python-Bibliothek SHAP zur Verfügung stellt.
Wie erzeugt man lokale Erklärungen mit der Python-Bibliothek SHAP?
Bei der lokalen Erklärbarkeit wird versucht, die Vorhersagen für einzelne Dateninstanzen zu erklären. Die mit SHAP berechneten Shapley-Werte sind an sich lokale Erklärungen, da sie für jede Vorhersage separat berechnet werden. Sie erklären, wie eine Vorhersage für eine bestimmte Instanz durch die Beiträge der einzelnen Merkmale zustande kommt. Um besser zu verstehen, wie sich die Merkmale auf eine einzelne Vorhersage unseres XGBoost-Modells auswirken, können wir Visualisierungen der Shapley-Werte wie Wasserfalldiagramme und Kraftdiagramme verwenden.
Sowohl das Wasserfall- als auch das Kraftdiagramm sind bereits in der Python-Bibliothek SHAP implementiert. Wir werden nun diese Visualisierungen verwenden, um die Vorhersage des Modells für die erste Instanz des Testdatensatzes (d. h. die erste Zeile des Testdatensatzes) zu erklären. Die approximierten Shapley-Werte für diese Vorhersage entsprechen dem ersten Eintrag in der Matrix der Shapley-Werte für den Testdatensatz, d. h. shap_values[0].
Wasserfalldiagramme
Wasserfalldiagramme (engl. waterfall plots) sind eine Möglichkeit, die Shapley-Werte einer lokalen Erklärung zu visualisieren. Eine der grundlegenden Eigenschaften der Shapley-Werte ist, dass die Summe aus Basiswert und Shapley-Werten der einzelnen Merkmale immer der Modellvorhersage entspricht. Wasserfalldiagramme stellen neben den positiven und negativen Beiträgen der einzelnen Merkmale auch diese additive Natur der Shapley-Werte dar. Sie zeigen also, wie ausgehend vom Basiswert durch Addition der Shapley-Werte der einzelnen Merkmale die Modellvorhersage erreicht wird.
Um ein Wasserfalldiagramm für die Shapley-Werte der Vorhersage für die erste Instanz des Testdatensatzes zu erstellen, wenden wir einfach die entsprechende Plot-Funktion der Bibliothek SHAP auf diese Shapley-Werte an:
# Visualize the Shapley values for the prediction of the first instance in the test dataset using a waterfall plot
# The waterfall plot shows how we get from shap_values.base_values to model.predict(X_test)[0]
shap.plots.waterfall(shap_values[0])
Das Wasserfalldiagramm in Abbildung 2 zeigt den Beitrag der verschiedenen Merkmale, um vom Basiswert (E[f(x)] = 2,044) im unteren Teil des Diagramms zur Modellvorhersage für diese Instanz (f(x) = 1,506) im oberen Teil des Diagramms zu gelangen. Die endgültige Vorhersage ergibt sich aus der Addition der Shapley-Werte der einzelnen Merkmale zum Basiswert, d. h. 2,044 + 0,02 -0,03 + 0,05 -0,06 +0,1 -0,39 +1,2 – 1,43 = 1,506 (ein kleiner Rundungsfehler ist zu berücksichtigen).
Interpretation des Wasserfalldiagramms
Das Wasserfalldiagramm ist wie folgt aufgebaut:
- Auf der x-Achse sind die Werte der Zielvariablen (in unserem Fall der Hauspreis) aufgetragen.
- Auf der y-Achse sind die Merkmalsnamen und die zugehörigen Merkmalsausprägungen für die betrachtete Instanz aufgetragen.
- Der Shapley-Wert jedes Merkmals für diese Instanz wird durch die Länge des Balkens angegeben.
- Die Farbe zeigt an, ob ein Merkmal einen positiven Beitrag (rot) oder einen negativen Beitrag (blau) leistet.
- Die Merkmale sind im Wasserfalldiagramm nach den absoluten Shapley-Werten geordnet. Der absolute Shapley-Wert gibt an, wie stark ein einzelnes Merkmal die Vorhersage beeinflusst hat.
Im obigen Beispiel sind die bei weitem wichtigsten Merkmale die Lage der Blockgruppe, d.h. der Längengrad und der Breitengrad. Während der Breitengrad zu einer überdurchschnittlichen Vorhersage beiträgt, schwächt der Längengrad diesen Effekt ab und trägt zu einer unterdurchschnittlichen Vorhersage bei. Die durchschnittliche Anzahl der Haushaltsmitglieder hat ebenfalls einen negativen Shapley-Wert (-0,39) und trägt zu einer unterdurchschnittlichen Vorhersage bei.
Die anderen Merkmale hatten einen relativ geringen Einfluss auf diese einzelne Vorhersage. Es ist jedoch zu beachten, dass die Shapley-Werte und die daraus gezogenen Schlussfolgerungen nur für diese eine Instanz gültig sind. Andere Instanzen des Datensatzes können völlig andere Shapley-Werte aufweisen.
Kraftdiagramme
Eine weitere Möglichkeit, die Shapley-Werte für einzelne Modellvorhersagen zu visualisieren, ist die Verwendung von Kraftdiagrammen (engl. force plots). Kraftdiagramme enthalten die gleichen Informationen wie Wasserfalldiagramme, stellen diese jedoch in einer komprimierteren Form dar. Kraftdiagramme können auch sehr einfach mit der entsprechenden Plot-Funktion der Python-Bibliothek SHAP erzeugt werden:
# For visualizations using force plots, the Javascript library must be loaded
shap.initjs()
# Visualize the Shapley values for the prediction of the first instance in the test dataset using a force plot
shap.plots.force(shap_values[0])
Im Kraftdiagramm ist die Modellvorhersage für diese Instanz hervorgehoben und fett gedruckt. Das Diagramm zeigt, wie der Einfluss der negativen und positiven Shapley-Werte zu dieser Vorhersage geführt hat, wobei die wichtigsten Merkmale und ihre Merkmalsausprägungen hervorgehoben sind. Auf der linken Seite sind die Merkmale mit positiven Shapley-Werten rot dargestellt. Auf der rechten Seite sind die Merkmale mit negativen Shapley-Werten blau dargestellt.
Die Darstellung im Kraftdiagramm entspricht somit einem Kräfteverhältnis zwischen Merkmalen mit positiven und Merkmalen mit negativen Shapley-Werten. Merkmale mit positiven Shapley-Werten entsprechen einer nach links ziehenden Kraft, Merkmale mit negativen Shapley-Werten entsprechen einer nach rechts ziehenden Kraft. Die endgültige Vorhersage erfolgt an dem Punkt, an dem sich die beiden Kräfte die Waage halten. Dabei wird natürlich auch der Basiswert berücksichtigt, der ebenfalls im Kraftdiagramm dargestellt ist.
Kraftdiagramme können auch verwendet werden, um die Shapley-Werte mehrerer Vorhersagen gleichzeitig darzustellen. Auf diese Weise können Kraftdiagramme auch für globale Erklärungen verwendet werden, die wir im nächsten Abschnitt behandeln.
Wie erstellt man globale Erklärungen mit der Python-Bibliothek SHAP?
Als nächstes werden wir die für den Testdatensatz berechneten Shapley-Werte verwenden, um das Gesamtverhalten unseres XGBoost-Modells zu verstehen. Globale Erklärungen helfen uns zu verstehen, wie sich das Modell insgesamt für alle Vorhersagen eines Datensatzes verhält. Im Falle der Shapley-Werte können wir so die wichtigsten Merkmale und ihre Auswirkungen auf die Vorhersagen des gesamten Datensatzes identifizieren.
Die berechneten Shapley-Werte selbst stellen zunächst nur lokale Erklärungen dar, d.h. sie erklären nur einzelne Vorhersagen. Globale Erklärungen für das gesamte Modell können jedoch erzeugt werden, indem die Shapley-Werte für alle Instanzen eines Datensatzes berechnet und anschließend in geeigneter Weise aggregiert oder visualisiert werden. Beispielsweise können wir Balken-, Schwarm- und Kraftdiagramme verwenden, um die globalen Auswirkungen von Merkmalen zu analysieren.
Balkendiagramme
Eine einfache Methode, sich einen Überblick über das Gesamtverhalten eines maschinellen Lernmodells zu verschaffen, ist die grafische Darstellung der Wichtigkeit jedes Merkmals in Form eines Balkendiagramms. Wenn die Merkmale nach ihrer Wichtigkeit geordnet sind, kannst Du schnell erkennen, welche Merkmale einen großen Einfluss auf die Vorhersagen des Modells haben. Du kannst ein solches Balkendiagramm ganz einfach mit Hilfe der Python-Bibliothek SHAP erstellen, indem Du die entsprechende Plot-Funktion auf die Matrix mit allen Shapley-Werten für unseren Testdatensatz anwendest:
# Visualize the Shapley values for the entire test dataset using a bar plot
shap.plots.bar(shap_values)
Das Balkendiagramm aggregiert die Shapley-Werte für jedes Merkmal, indem der Durchschnitt der absoluten Shapley-Werte für das entsprechende Merkmal berechnet wird. Dahinter steht die Überlegung, dass Merkmale mit hohen absoluten Shapley-Werten für die Vorhersagen des Modells wichtig sind. Dabei spielt es keine Rolle, ob sich ein Merkmal positiv oder negativ auf die Modellvorhersagen auswirkt.
Da wir an der globalen Bedeutung der Merkmale interessiert sind, bilden wir den Mittelwert der absoluten Shapley-Werte pro Merkmal über alle Instanzen des Testdatensatzes. Der durchschnittliche absolute Shapley-Wert für jedes Merkmal wird im Diagramm rechts neben dem entsprechenden Balken für das Merkmal dargestellt. Die Merkmale sind nach der Größe des durchschnittlichen absoluten Shapley-Wertes absteigend geordnet. Das bedeutet, dass die Merkmale mit dem größten Einfluss auf das Modell ganz oben im Balkendiagramm dargestellt werden, während die Merkmale mit dem geringsten Einfluss weiter unten im Balkendiagramm dargestellt werden.
In unserem Beispiel sehen wir, dass der Breitengrad und der Längengrad der Blockgruppen den größten Einfluss auf das Modell haben. Der Breitengrad trägt im Durchschnitt ±0,85 zum vorhergesagten Hauspreis bei, der Längengrad ±0,72. Darüber hinaus haben auch die Merkmale „MedInc“, „AveOccup“ sowie „AveRooms“ einen größeren Einfluss auf die Vorhersagen des Modells. Der Einfluss der anderen drei Merkmale ist dagegen im Durchschnitt eher gering.
Balkendiagramme für Datensätze mit vielen Merkmalen
Wenn Du mit einem Datensatz arbeitest, der sehr viele Merkmale enthält, kann ein solches Balkendiagramm schnell lang und unübersichtlich werden. In diesem Fall kannst Du mit dem Parameter „max_display“ einstellen, wie viele Balken im Balkendiagramm angezeigt werden sollen. Die Beiträge der weniger wichtigen Merkmale werden dann einfach aufsummiert und zusammen in einem Balken dargestellt:
# The max_display parameter can be used to set the maximum number of bars to be displayed in the bar plot
shap.plots.bar(shap_values, max_display=6)
Balkendiagramme geben einen ersten Überblick über das Gesamtverhalten eines Modells. Sie geben jedoch nur Auskunft über die Wichtigkeit der einzelnen Merkmale. Im Folgenden werden wir uns daher mit Schwarmdiagrammen befassen, die die Shapley-Werte für einen Datensatz wesentlich informativer darstellen.
Schwarmdiagramme
Eine weitere Möglichkeit, das Gesamtverhalten eines Modells besser zu verstehen, ist die Darstellung der Shapley-Werte als Schwarmdiagramm (engl. beeswarm plot). Schwarmdiagramme sind komplexer als Balkendiagramme. Sie sind aber auch wesentlich informativer. Anstatt die Shapley-Werte eines Datensatzes zu aggregieren, stellen sie die gesamte Verteilung der Shapley-Werte für jedes Merkmal dar. Auf diese Weise geben Schwarmdiagramme nicht nur Aufschluss über die relative Wichtigkeit der einzelnen Merkmale, sondern zeigen auch, wie sich unterschiedliche Merkmalsausprägungen auf die Modellvorhersagen auswirken.
Schwarmdiagramme sind in der Python-Bibliothek SHAP bereits implementiert. Du kannst sie mit folgendem Befehl erzeugen:
# Visualize the Shapley values for the entire test dataset using a beeswarm plot
shap.plots.beeswarm(shap_values)
Abbildung 6 zeigt das Schwarmdiagramm für unser Beispiel der Hauspreise in Kalifornien.
Aufbau des Schwarmdiagramms
Schwarmdiagramme stellen die Shapley-Werte der verschiedenen Merkmale für alle Instanzen eines Datensatzes dar. Das bedeutet, dass jeder Punkt im Diagramm den Shapley-Wert eines Merkmals für eine bestimmte Instanz des Datensatzes darstellt. Die Struktur des Schwarmdiagramms ist wie folgt:
- Die Merkmale sind auf der y-Achse in absteigender Reihenfolge ihrer globalen Bedeutung dargestellt. Das Merkmal mit dem größten Einfluss auf die Modellvorhersagen steht also ganz oben, das Merkmal mit dem geringsten Einfluss ganz unten.
- Auf der x-Achse sind die Shapley-Werte aufgetragen. Die horizontale Position der Punkte gibt also an, wie groß ihr Einfluss auf die Modellvorhersage ist und ob sie diese positiv oder negativ beeinflussen.
- Bei der Darstellung der Shapley-Werte wird auch deren Dichte berücksichtigt. Das heißt, wenn für viele Instanzen Shapley-Werte der gleichen Größenordnung auftreten (sich also einzelne Punkte überlappen), werden die Punkte in Richtung der y-Achse gestreut. Dies führt zu einem besseren Verständnis der Verteilung der Shapley-Werte für die verschiedenen Merkmale.
- Die Größenordnung der Merkmalsausprägungen wird im Schwarmdiagramm farblich hervorgehoben. Shapley-Werte für Instanzen mit einer hohen Merkmalsausprägung für das betreffende Merkmal (im Vergleich zu den anderen Instanzen) werden rot dargestellt. Shapley-Werte für Instanzen mit niedrigen Merkmalsausprägungen werden blau dargestellt.
Interpretation des Schwarmdiagramms
Mit Hilfe von Schwarmdiagrammen lassen sich Zusammenhänge zwischen der Ausprägung einzelner Merkmale und deren Einfluss auf die Modellvorhersagen erkennen. So zeigt sich in unserem Beispiel, dass eine hohe durchschnittliche Anzahl von Räumen pro Haushalt (d.h. hohe Merkmalsausprägungen für „AveRooms“) überwiegend mit positiven Shapley-Werten einhergeht und damit in der Regel zu einer überdurchschnittlichen Hauspreisprognose beiträgt.
Im Gegensatz dazu sind Instanzen mit niedrigen Werten für das Merkmal „AveRooms“ überwiegend mit negativen Shapley-Werten verbunden und tragen somit zu einer unterdurchschnittlichen Prognose bei. Daraus können wir schließen, dass das Merkmal „AveRooms“ positiv mit den prognostizierten Hauspreisen korreliert. Umgekehrt verhält es sich mit dem Breitengrad. Hier führen höhere Breitengrade zu niedrigeren Hauspreisprognosen.
Darüber hinaus gibt die Verteilung der Punkte weitere Hinweise auf den Zusammenhang zwischen den Merkmalsausprägungen und den Modellvorhersagen. So zeigt das Merkmal „MedInc“ eine dichte Konzentration von Instanzen mit niedrigem Medianeinkommen (blaue Punkte), die leicht negative Shapley-Werte aufweisen, also einen leicht negativen Einfluss auf den vorhergesagten Hauspreis haben.
Bei den Instanzen mit hohem Medianeinkommen (rote Punkte) sind die Shapley-Werte dagegen überwiegend positiv und auf der x-Achse deutlich breiter gestreut. So gibt es hier sowohl Fälle mit einem geringen positiven Einfluss auf den vorhergesagten Hauspreis als auch Fälle mit einem sehr starken positiven Einfluss auf die Modellvorhersage. Daraus können wir schließen, dass ein hohes Medianeinkommen einen stärkeren positiven Einfluss auf den vorhergesagten Hauspreis hat als ein niedriges Medianeinkommen einen negativen Einfluss.
Kraftdiagramme
Wie Du bereits weißt, können Kraftdiagramme verwendet werden, um Shapley-Werte für lokale Erklärungen zu visualisieren. Kraftdiagramme können jedoch auch verwendet werden, um globale Erklärungen zu generieren. Kraftdiagramme für globale Erklärungen zeigen, wie der Einfluss von negativen und positiven Shapley-Werten zu den unterschiedlichen Vorhersagen für die Instanzen eines Datensatzes geführt hat.
Um ein globales Kraftdiagramm zu erstellen, wird zunächst für jede Instanz eines Datensatzes ein lokales Kraftdiagramm erstellt (wie in Abbildung 3 dargestellt). Alle diese lokalen Kraftdiagramme werden dann um 90 Grad gedreht und horizontal gestapelt. Auf diese Weise entsteht ein neues Kraftdiagramm, das die Kraftdiagramme der einzelnen Instanzen zusammenfasst und eine globale Erklärung für das Modell liefert.
Kraftdiagramme für globale Erklärungen können ebenfalls sehr einfach mit der entsprechenden Plot-Funktion der Python-Bibliothek SHAP erzeugt werden. Im Folgenden erzeugen wir das globale Kraftdiagramm jedoch nur für die ersten 100 Instanzen des Testdatensatzes, da die Erstellung des Diagramms bei mehreren tausend Instanzen sehr langsam ist.
# Visualize the Shapley values for the entire test dataset using a force plot
shap.plots.force(shap_values[0:100])
Abbildung 7 zeigt das Kraftdiagramm für unser Beispiel.
Aufbau des Kraftdiagramms
Das Kraftdiagramm für globale Erklärungen aus der Python-Bibliothek SHAP ist interaktiv. Das globale Kraftdiagramm ist wie folgt aufgebaut:
- Die Werte der Modellvorhersagen werden auf der y-Achse dargestellt. Da das Diagramm interaktiv ist, können die auf der y-Achse dargestellten Werte jedoch geändert werden. So können z.B. statt der Werte der Modellvorhersagen auch die Effekte der einzelnen Merkmale auf der y-Achse dargestellt werden.
- Auf der x-Achse werden die verschiedenen Instanzen aufgetragen. In unserem Beispiel reicht die x-Achse von 0 bis 99, da wir die Shapley-Werte für insgesamt 100 Instanzen visualisiert haben. Die horizontale Position der Instanzen ist standardmäßig nach ihrer Ähnlichkeit in Bezug auf ihre Shapley-Werte geordnet. Die Reihenfolge der Instanzen kann jedoch geändert werden. So können die Instanzen auch nach ihrer ursprünglichen Reihenfolge im Datensatz, nach dem Wert ihrer Modellvorhersage oder nach den Merkmalsausprägungen einzelner Merkmale sortiert werden.
- Verschiedene Instanzen können interaktiv ausgewählt werden. Wurde eine Instanz ausgewählt, so wird neben dem Index der Instanz in der gewählten Reihenfolge auch die Modellvorhersage sowie die Merkmalsausprägungen der wichtigsten Merkmale für diese Instanz angezeigt. Den Originalindex der Instanz kann man sich durch Anklicken der Instanz anzeigen lassen. Die farbliche Darstellung der Merkmalsausprägungen der Instanz zeigt an, ob die Merkmale einen negativen Shapley-Wert (blau) oder einen positiven Shapley-Wert (rot) aufweisen.
- Die Ausprägung der Shapley-Werte für die verschiedenen Merkmale wird im globalen Kraftdiagramm farblich hervorgehoben. Im unteren Teil des Diagramms sind diejenigen Merkmalsausprägungen rot dargestellt, die positive Shapley-Werte aufweisen und somit die Vorhersage erhöhen. Im oberen Teil des Diagramms sind dagegen die Merkmalsausprägungen mit negativen Shapley-Werten, die die Vorhersage verringern, blau dargestellt.
Ein Kraftdiagramm für globale Erklärungen ermöglicht es Dir, interaktiv die Zusammenhänge zwischen den Merkmalsausprägungen der einzelnen Merkmale und deren Einfluss auf die Modellvorhersagen zu erkunden. Damit bietet das Kraftdiagramm noch einmal deutlich mehr Informationen als das Balkendiagramm oder das Schwarmdiagramm. Allerdings lassen sich die Informationen im Kraftdiagramm nicht auf einen Blick erfassen, sondern sind mit einer zeitintensiveren Analyse verbunden.
Vollständiger Python-Code für diesen Artikel
Alle Codezeilen dieses Tutorials sind im nachfolgenden Codeblock zusammengefasst. Es lohnt sich auch, einen Blick in das folgende Jupyter-Notebook auf Github oder in dieses Google Colab-Notebook zu werfen.
# # 1. Import all required libraries
# We use the SHAP library to estimate and visualize Shapley values
import shap
# We use the XGBoost implementation from the xgboost library
import xgboost
# We use this function from the Scikit-learn library to split our dataset into a training dataset and a test dataset
from sklearn.model_selection import train_test_split
# We use this function from the Scikit-learn library to compute the mean squared error of the model's predictions
from sklearn.metrics import mean_squared_error
# # 2. Load the sample dataset
# Load the California housing dataset (https://www.dcc.fc.up.pt/~ltorgo/Regression/cal_housing.html)
# X is the features and y is the targets
X, y = shap.datasets.california()
# Split the dataset into a training dataset and a test dataset, using 80% of the instances for the training dataset and 20% of the instances for the test dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# # 3. Train an XGBoost model
# Initialize an XGBoost model for regression tasks
model = xgboost.XGBRegressor()
# Train the XGBoost model on the training dataset
model.fit(X_train, y_train)
# Make predictions on the test dataset using the XGBoost model
predictions = model.predict(X_test)
# Calculate the prediction error for the test dataset using the mean squared error
mse = mean_squared_error(y_test, predictions)
print(f"MSE: {mse}")
# # 4. Explain the XGBoost model using the SHAP library
# ## 4.1. Estimate the Shapley values
# Initialize an explainer that estimates Shapley values using SHAP
# Here we use the training dataset X_train to compute the base value
explainer = shap.Explainer(model=model, masker=X_train)
# As you can see below, the Tree SHAP algorithm is used to estimate the Shapley values
# Tree SHAP is a method specifically designed for tree models and tree ensembles that estimates Shapley values quickly and accurately.
explainer.__class__
# Estimate the Shapley values for the test dataset
shap_values = explainer(X_test)
# ## 4.2. Local explanations
# Local explanations are explanations for individual predictions of the model
# ### Waterfall Plot
# Visualize the Shapley values for the prediction of the first instance in the test dataset using a waterfall plot
# The waterfall plot shows how we get from shap_values.base_values to model.predict(X_test)[0]
shap.plots.waterfall(shap_values[0])
# ### Force Plot
# For visualizations using force plots, the Javascript library must be loaded
shap.initjs()
# Visualize the Shapley values for the prediction of the first instance in the test dataset using a force plot
shap.plots.force(shap_values[0])
# ## 4.3. Global explanations
# Global explanations describe the overall behavior of the model
# ### Bar Plot
# Visualize the Shapley values for the entire test dataset using a bar plot
shap.plots.bar(shap_values)
# The max_display parameter can be used to set the maximum number of bars to be displayed in the bar plot
shap.plots.bar(shap_values, max_display=6)
# ### Beeswarm Plot
# Visualize the Shapley values for the entire test dataset using a beeswarm plot
shap.plots.beeswarm(shap_values)
# ### Force Plot
# Visualize the Shapley values for the entire test dataset using a force plot
shap.plots.force(shap_values[0:100])Weiterführende Literatur
In diesem Abschnitt findest Du weiterführende Literatur, die Dir helfen wird, tiefer in das Thema SHAP und die Visualisierung von Shapley-Werten einzusteigen.
Bücher
Wissenschaftliche Publikationen
- Lundberg, Scott M., and Su-In Lee. “A unified approach to interpreting model predictions.” Advances in Neural Information Processing Systems (2017).
- Lundberg, Scott M., et al. „Explainable machine-learning predictions for the prevention of hypoxaemia during surgery.“ Nature biomedical engineering 2.10 (2018): 749-760.
- Lundberg, Scott M., et al. „From local explanations to global understanding with explainable AI for trees.“ Nature machine intelligence 2.1 (2020): 56-67.
Artikel
Zusammenfassung
In diesem Blogbeitrag hast Du gelernt, wie man die Python-Bibliothek SHAP verwenden kann, um die Funktionsweise von maschinellen Lernverfahren zu erklären.
Konkret hast Du gelernt:
- Um Feature-Attributionen mit der Python-Bibliothek SHAP zu berechnen, kannst Du in der Regel einfach den allgemeinen Explainer verwenden, der automatisch die passende SHAP-Methode für Deine Daten und Dein Modell auswählt.
- Lokale Erklärungen kannst Du mit Hilfe von Wasserfall- und Kraftdiagrammen erstellen.
- Globale Erklärungen kannst Du mit Hilfe von Balken-, Schwarm- und Kraftdiagrammen erstellen.
Hast Du noch Fragen?
Schreibe Deine Fragen gerne unten in die Kommentare und ich werde mein Bestes tun, sie zu beantworten.
P.S.: Natürlich freue ich mich auch über konstruktives Feedback zu diesem Blogpost 😊

Hallo, mein Name ist René Heinrich. Ich bin Data Scientist und promoviere im Bereich der vertrauenswürdigen künstlichen Intelligenz. Auf diesem Blog teile ich meine Erfahrungen und alles, was ich auf meiner eigenen Wissensreise gelernt habe.



